I’ve finished the basic guts of the CPLD CPU, and it works! It’s still missing roughly half of the intended CPU functionality, but what’s there now is still a usable CPU. I’ve implemented jumps, conditional branching, set/clear of individual ALU flags, bitwise logical operators, addition, subtraction, compare, and load/store of the accumulator from memory. The logical and mathematical functions support immediate operands (literal byte values) as well as absolute addressing for operands in memory. Not too shabby! Not yet implemented are the X register, indexed addressing, the stack, JSR/RTS, increment, decrement, and shift.

I wrote a verification program to exercise all the instructions in all the supported modes, which I re-run after every design change to make sure I didn’t break anything. Here’s a screenshot of the verification program in ModelSim, which doesn’t really demonstrate anything useful, but looks cool. You can grab my Verilog model, testbench, and verification program here. Comments on my Verilog structure and style are welcome.

Now for the bad news. The design has consumed far more CPLD resources than I’d predicted. I’m targeting a 128 macrocell device, but the half-finished CPU I’ve got now already consumes 132. By the time it’s done, it might be twice that many. While I think my original accounting of macrocells needed for registers and state data was accurate, it looks like I greatly underestimated how many macrocells would be required for random logic. For example, after implementing the add instruction, the macrocell count jumped by 27!  That’s almost 25% of the whole device, for a single instruction.

I’m finding it difficult to tell if the current macrocell total is high because I’m implementing a complex CPU, or because I’m implementing a simple CPU in a complex way. Could I get substantial macrocell savings by restructuring some of the Verilog code, without changing the CPU functionally? It’s hard to say, but I think I could. Looking at the RTL Model and Technology Map View is almost useless– they’re just incomprehensible clouds of hundreds of boxes and lines. Yet deciphering these is probably what I need to do, if I want to really understand the hardware being synthesized from my Verilog code, and then look for optimizations.

The Verilog code is written in a high-level manner, specifying the movement of data between CPU registers, but without specifying the logic blocks or busses used to accomplish those movements. These are left to be inferred by the synthesis software. For example, the add, subtract, and compare instructions could conceivably all share a single 8-bit adder. So do they? The Verilog code doesn’t specify, but I think the synthesis software inferred separate adders. On the surface this seems bad, but I learned in my previous experiments that the software is generally smarter than I am about what logic structures to use. Still, I’ll try restructuring that part of the code to make it clear there’s a single shared adder, and see if it helps or hurts.

The core of the code is a state machine, with a long always @* block implementing the combinatorial logic used to determine the next values for each register, each clock cycle. There are 10 unique states. The clever encoding of the 6502’s conditional branching and logic/math opcodes (which I’m following as a guide) allowed me to implement 24 different instructions with just a handful of states.

Verilog NOT Operator, and Order of Operations

I encountered a mystery while working on the CPU design. I attempted to aid the synthesis software by redefining subtraction in terms of addition:

    { carryOut, aNext } = a + ~dataBus + carryIn;

This works because a – b is the same as a + not(b) + 1.  If carryIn is 1, then subtraction can be performed with an adder and eight inverters. Fortunately the CPLD already provides the normal and inverted versions of all input signals, so the bitwise NOT is effectively free. I was very surprised to find that the above code does not work! It computes the correct value for aNext, but carryOut is wrong. The following code, however, does work as expected:

    { carryOut, aNext } = a + {~dataBus[7], ~dataBus[6], ~dataBus[5], ~dataBus[4], ~dataBus[3], ~dataBus[2], ~dataBus[1], ~dataBus[0]} + carryIn;

Now how is that second line different from the first? I would have said they were completely equivalent, yet they are not. The difference seems to be some subtlety of Verilog’s rules for sign-extending values of different lengths when performing math with them.

Even stranger, I found that the order in which I listed the three values to be summed made a dramatic difference. Hello, isn’t addition associative? Apparently not, in the bizarro world of Verilog:

    { carryOut, aNext } = a + ~dataBus + carryIn; // design uses 131 macrocells
    { carryOut, aNext } = carryIn + a + ~dataBus; // design uses 151 macrocells
    { carryOut, aNext } = carryIn + ~dataBus + a; // design uses 149 macrocells

I’ve been planning to use an Altera Max 7128S for this CPLD – CPU project, because at 128 macrocells it’s the largest commonly-available CPLD that I could find in a PLCC package. Yesterday, however, I started wondering how the competition from Xilinx stacked up. Even if I couldn’t get as large a device (108 macrocells max in a PLCC package), maybe the Xilinx device architecture allowed for denser logic, more product terms per macrocell, or some other factor that might permit it to do more with less. So I read through the details of the Xilinx XC95108 CPLD datasheet, comparing it to the Altera EPM7128S CPLD, to see how they differed.

What I found nearly made me laugh out loud. They are the same. Not just similar, but virtually identical in their internal architectural details. All the marketing terms and sales claims make it sound as if each vendor has some amazing technological advantage, but it’s all just hype. Inside, when you look at how these devices work internally, there’s no meaningful difference I could find. What’s more, the descriptive text of the two datasheets is so similar, if this were a school project, they’d be hauled in front of the disciplinary committee on plagiarism charges.

Take a look at the Altera diagram of one of their macrocells. You’ve got a logic array on their left with 36 inputs, five product terms feeding into a selection matrix. Additional product terms from other macrocells can also feed into the matrix if needed. The output goes to set of OR/XOR gates, and then either to a flip-flop, or bypasses the flip-flop and exits the macrocell. Product terms can also be used as clock, preset, clear, and enable control signals for the flip-flop, or global signals can be used for those controls.

Now take a look at the diagram of a Xilinx macrocell. Look familiar? 36-Entry logic array, five product terms, optional expansion terms from other macrocells, OR/XOR gates, flip-flop with bypass, and choice of product terms or global signals for clock, preset, clear, and enable. It’s almost an exact copy of the first diagram. It’s like a children’s game of “find five differences between these pictures”.

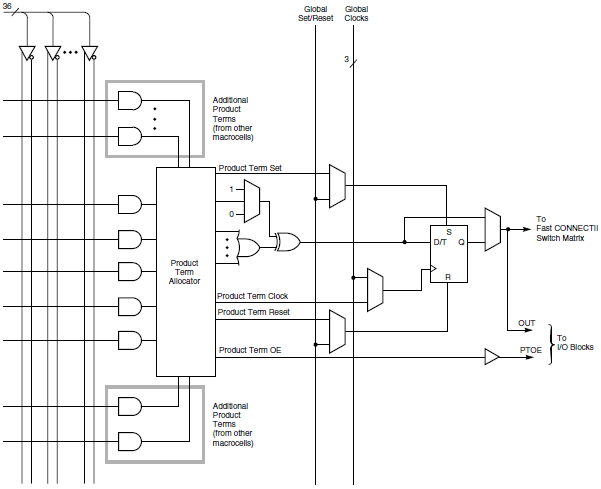
OK, there are some minor differences, like Altera’s “expander” product terms, and the exchange of a clock enable for an output enable signal.  But you have to admit these diagrams are so similar, they could have been made by the same person. They even make the same arbitrary choices for orientation and position of the elements in the diagram.

Now compare the accompanying text. First, Altera’s: “Combinatorial logic is implemented in the logic array, which provides five product terms per macrocell. The product-term select matrix allocates these product terms for use as either primary logic inputs (to the OR and XOR gates) to implement combinatorial functions, or as secondary inputs to the macrocell’s register clear, preset, clock, and clock enable control functions.”

And here’s Xilinx’s text: “Five direct product terms from the AND-array are available for use as primary data inputs (to the OR and XOR gates) to implement combinatorial functions, or as control inputs including clock, set/reset, and output enable. The product term allocator associated with each macrocell selects how the five direct terms are used.”

Don’t those seem more than just a little bit similar? I mean, there’s a long clause that’s almost word-for-word identical, including the choice to use a parenthetical expression: “for use as [either] primary [logic/data] inputs (to the OR and XOR gates) to implement combinatorial functions, or as [secondary/control] inputs”. That can’t be a coincidence.

I decided to take the advice I gave myself in the comments of my previous post, and actually synthesize the three Verilog adder examples to see what would happen. I tried each of the examples under Quartus II Web Edition 9.0, set to optimize for area. The size of a, b, c, d0, d1, and d2 was chosen as 8 bits.

1.  44 macrocells. Yes, it created 3 separate dedicated adders. The RTL showed three registers for d0, d1, d2, each with a mux leading into it, as well as the adders and a single decoder for state. The Technology Map Viewer showed 24 mc’s used by the registers, and 20 mc’s total by the three adders.

2.  This design is broken. By not specifying default values for in1 and in2, the software inferred a latch for them in the hypothetical s3 state. After fixing that, the design consumed 52 macrocells. Again the RTL showed three registers for d0, d1, d2, each with a mux leading into it. It showed a single adder, with 2 cascaded muxes at each adder input. It also showed a decoder and a stray OR gate. The Technology Map Viewer showed 24 mc’s used by the registers, 27 by the single adder, and 1 more that I couldn’t exactly account for– part of one of the muxes maybe.

3.  This design is also broken in the same way as #2. There’s also a copy-paste error in the enable signal in s2 state. After fixing those mistakes, the design consumed 52 macrocells. The RTL looked very similar to #2, and the Technology Map View was identical to #2.

There’s a lot to investigate further here, such as how the single adder in #2 could require 27 mc’s when the three adders in #1 only require a combined total of 20 mc’s. But the major conclusion is that all my attempts at “improving” the design only made the results worse.

I’m having some trouble finding the best way to structure the Verilog code for this CPU. In particular, I’ve encountered one small headache and one larger one.

The small headache relates to the best way to describe complex combinatorial logic that doesn’t involve any registers. Consider some hypothetical logic that determines the value of the incrementPC and loadA control signals, based on the current state. One way to do this would be:

    wire incrementPC, loadA;
    assign incrementPC = (state == s1) || (state == s3) || (state == s4);
    assign loadA = (state == s0) || (state == s2) || (state == s4);


That works fine, and it’s pretty clear what it does. But for more complex designs, it’s clearer to use procedural assignment and a case statement, grouping all of the control signals for each state together:

    reg incrementPC, loadA;
 
    always @* begin
        case (state)
            s0:
                incrementPC = 1'b0;
                loadA = 1'b1;
                // other control signals...
            s1:
                incrementPC = 1'b1;
                loadA = 1'b0;
 
                // other control signals...
            s2:
                incrementPC = 1'b0;
                loadA = 1'b1;
                // other control signals...
            s3:
                incrementPC = 1'b1;
                loadA = 1'b0;
                // other control signals...
 
            s4:
                incrementPC = 1'b1;
                loadA = 1'b1;
                // other control signals...
        endcase
    end

The problem with this approach is visible in the first line: incrementPC and loadA must be declared as type “reg”, even though they are not registers. During synthesis, no register will be created as long as your code is correct, but Verilog demands that the target of a procedural assignment like this always be type “reg”. So reg does not always mean that something is a register. I find this very confusing and misleading, because it means you can’t just look at the Verilog code to see which signals are registers and which are purely combinatorial.

My bigger problem is more subtle, and is about good HDL design practices rather than any quirk of the Verilog standard. I’m unsure how explicit I should be in defining the structure of the virtual hardware described by the Verilog code. At one extreme, I could write a high-level functional description of *what* the CPU does, ignoring *how* it does it, and leave the Synthesis software to figure it out. Or at the other extreme, I could work out a block diagram of the CPU consisting of familiar real-world elements like registers, arithmetic unit, muxes, and busses, and then write Verilog code to describe these elements and how they’re all connected.

To help make this distinction clearer, here’s an example based on section 6.2.4 of the book FPGA Prototyping by Verilog Examples. Imagine a state-driven system that can add two input registers, and store the output in a third register. One way to describe this would be high-level, functional:

    always @(posedge clk) begin
        case (state)
            s0:
                d0 <= a + b;               s1:                 d1 <= b + c;             s2:                 d2 <= a + c;         endcase     end     
Great, that's compact and clear. But what does the datapath of this hardware look like? Is there one adder unit, or three? Who knows? It's a black box, relying entirely on the synthesis software to do the right thing.

A second approach would be to explicitly define a single adder unit:

    assign mout = in1 + in2;
    
    always @* begin
        // default: maintain same values
        d0_next = d0;
        d1_next = d1;
        d2_next = d2;
        
 
        case (state)
            s0:
                begin
                    in1 = a;
                    in2 = b;
                    d0_next = mout;
                end
            s1:
                begin
 
                    in1 = b;
                    in2 = c;
                    d1_next = mout;
                end
            s2:
                begin
                    in1 = a;
                    in2 = c;
                    d2_next = mout;
 
                end
        endcase
    end
    
    always @(posedge clk) begin
        d0 <= d0_next;         d1 <= d1_next;         d2 <= d2_next;       end     
That makes the hardware design clearer, so it's unambiguous that there's only one adder. Is this second approach better than the first, then? Mabye, maybe not. If you're optimizing for space, and don't trust the synthesis software to be as smart as you are, then the second example is probably better. But if you're optimizing for speed, having three separate adders (or at least the possibility of three) may actually be better.

Even this second design is somewhat ambiguous. Presumably there are some muxes at the input to the adder, and a mux or load enable at the input to each D register too. But the Verilog code leaves this all implied and unspecified. Here's a third example that spells everything out in full detail:

    wire [1:0] in1Select, in2Select;
 
    assign in1 = (in1Select == 2'b00) ? a :
        (in1Select == 2'b01) ? b :
        (in1Select == 2'b10) ? c :
        d;
    assign in2 = (in2Select == 2'b00) ? a :
        (in2Select == 2'b01) ? b :
        (in2Select == 2'b10) ? c :
        d;
    
 
    assign mout = in1 + in2;
    
    wire loadEnableD0;
    wire loadEnableD1;
    wire loadEnableD2;
    
    always @* begin
        // default: disable all loads
        loadEnableD0 = 1'b0;
        loadEnableD1 = 1'b0;
 
        loadEnableD2 = 1'b0;
        case (state)
            s0:
                begin
                    in1Select = 2'b00;
                    in2Select = 2'b01;
                    loadEnableD0 = 1'b1;
                end
            s1:
 
                begin
                    in1Select = 2'b01;
                    in2Select = 2'b10;
                    loadEnableD1 = 1'b1;
                end
            s2:
                begin
                    in1Select = 2'b00;
                    in2Select = 2'b10;
 
                    loadEnableD1 = 1'b1;
                end
        endcase
    end
    
    always @(posedge clk) begin
        if (loadEnableD0)
            d0 <= mout;         if (loadEnableD1)               d1 <= mout;         if (loadEnableD2)             d2 <= mout;     end     
This approach makes it very clear what's happening in terms of the hardware, and you could build an equivalent physical circuit from 7400 parts. Is this better or worse than the other two approaches? I find it better in terms of understanding what will be synthesized, but it's worse in terms of length. I also suspect that by specifying all the details in this way, it may be over-constraining the synthesis software, preventing it from using some clever optimizations to pack the same amount of logic into less space.

I find myself going around in circles with variations of these three approaches, unable to really get started with the actual CPU design work.

I’ve made a little bit of progress on the CPU in a CPLD project. As mentioned previously, this will be an 8-bit CPU with a 10-bit address space, targeting a 128 macrocell CPLD. The instruction set will be a simplified version of BMOW’s, which itself was a close cousin of the 6502 instruction set. Exactly how “simplified” it needs to be in order to fit remains to be seen, but I’m planning to omit the Y register, zero page, and indirect addressing modes. It will still have A and X registers, a hardware stack pointer, and all the “standard” opcodes in immediate, absolute, and indexed addressing modes. I’ve mostly just been planning and not writing much Verilog yet, but after fleshing out the datapath and a tiny bit of control logic, I’ve used 73 macrocells so far.

Working with the Altera software has been pretty good so far, and I’ve been much less frustrated than when I was working with the Xilinx software to create 3DGT from an FPGA. I’m not sure if that’s the software itself, or simply that I’m working on a simpler project and a simpler device, but it’s a welcome change.

I found a couple of similar CPU projects that might provide some inspiration:

MCPU – http://www.opencores.com/project,mcpu – A very tiny CPU that fits in a 32 macrocell CPLD. It has a single 8-bit register, and just a 6-bit (64 word) address space. It also has only four instructions: NOR, ADD, store, and conditional jump. Yet with combinations of those instructions, you can do some pretty complicated stuff. Very clever! Check it out.

MPROZ – http://www.unibwm.de/ikomi/pub/mproz/mproz_e.pdf – MCPU borrows its instruction set from here. MPROZ has a 15-bit address space, but NO data registers. All computation is done directly on locations in memory. It also does MCPU one better by having only three instructions: NOR, ADD, and branch. It fits in an FPGA with 484 macrocells.

OK, the CPU design spark is back, sooner than I’d expected. I have an urge to implement a minimal CPU using a CPLD. If you’re not familiar with the term, a CPLD is a simple programmable logic chip, existing somewhere on the complexity scale between PALs (like the 22V10’s I used in BMOW) and FPGAs. Typically a CPLD has a similar internal structure to PALs, with macrocells containing a single flip-flop and some combinatorial logic for sum-of-products expressions. They are also non-volatile like PALs. Yet typical CPLDs contain 10x as many macrocells as a PAL, with some macrocells used for internal purposes and not connected to any pin. FPGAs are generally much larger and more complex, with thousands of macrocells and specialized hardware blocks for tasks like multiplication and clock synthesis. FPGAs also normally contain some built-in RAM, and are themselves RAM-based, requiring configuration by some other device whenever power is applied.

I’m attracted to CPLD’s because I’m hoping they’ll provide a good step up from PAL’s, without drowning me in FPGA complexity, as happened when I worked on 3D Graphics Thingy.  I’m pretty confident I can figure out how to work with CPLD’s without driving myself crazy, increasing the chances that I might actually finish this project. Given the limited hardware resources of CPLD’s, fitting a CPU will also be an interesting challenge.

I’ve also been wanting to design my own custom PCB’s for quite some time, and this will give me an opportunity. The end goal of this project will be a single-board computer on a custom PCB, with my CPLD-CPU, RAM, ROM, some input buttons/switches, and some output LEDs/LCD. I need to limit myself to CPLD’s that come in a PLCC package, so I can use a through hole socket and solder it myself. Unfortunately that will limit my choices pretty severely. I think it’s theoretically possible to hand-solder the more common TQFP surface-mount package, but I’m not excited to try it. And for other package types, forget it.

Here’s some back-of-the envelope figuring to get the ball rolling. This is assuming an 8-bit CPU with a 10-bit address space (1K).

I/O pins needed:

• 8 data bus
• 10 address bus
• 1 clock
• 1 /reset
• 1 /irq
• 1 read-write
• ~4 chip selects for RAM, ROM, peripherals

That’s 26 I/Os. So a PLCC-44 package should be fine, as CPLDs in that package typically have about 34 I/Os.

Macrocells needed for holding CPU state:

• 10 program counter
• 10 stack pointer
• 10 scratch/address register
• 8 opcode register
• 3 opcode phase
• 8 accumulator
• 8 index register
• 3 ALU condition codes

That’s 60.

Then I’ll need some macrocells for combinatorial logic. This is a lot harder to predict, and in many cases I should be able to use the combinatorial logic resources and the flip-flop from a single macrocell. I’ll just pull some numbers out of thin air.

Macrocells needed for combinatorial logic:

• 16? arithmetic/logic unit (8-bit add, AND, OR, shift, etc)
• 16? control/sequencing logic
• ??? other stuff I forgot

So that’s a grand-total of 92 macrocells for everything.

If I shrunk the address space down, and maybe changed to a 4-bit word size, I might be able to fit it in a 64 macrocell CPLD. But more than likely, it seems I’ll be looking for a CPLD in the 100 to 128 macrocell range. Considering my requirement for PLCC packaging, that will limit the choices to two or three possibilities, but more on that later.

I think the most challenging part of this project will be the control/sequencing logic, and the assignment of opcodes. BMOW was microcoded, and used a separate microcode ROM to execute a 16-instruction microprogram to implement each CPU instruction. In this case, I’ll need to create dedicated combinatorial logic to drive all the enables, selects, and other inputs in the right sequence to ferry data around the CPU to execute the instructions. Doing this with minimal logic will be a real challenge, and undoubtedly I’ll be using the bits of the opcode itself to derive many of those control signals.